Interpreting the Intercept in a Regression Model
Interpreting the intercept in a regression model isn’t always as straightforward as it looks.
Here’s the definition: the intercept (often labeled the constant) is the expected value of Y when all X=0. But that definition isn’t always helpful. So what does it really mean?
Regression with One Predictor X
Start with a very simple regression equation, with one predictor, X.
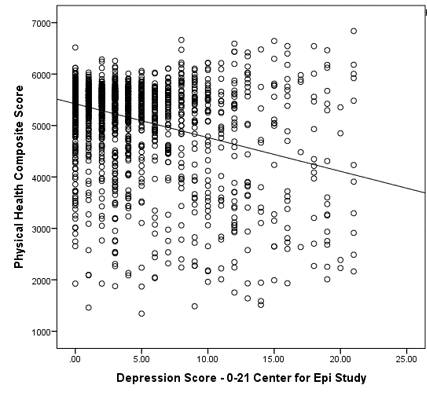
If X sometimes equals 0, the intercept is simply the expected value of Y at that value. In other words, it’s the mean of Y at one value of X. That’s meaningful.
If X never equals 0, then the intercept has no intrinsic meaning. You literally can’t interpret it. That’s actually fine, though. You still need that intercept to give you unbiased estimates of the slope and to calculate accurate predicted values. So while the intercept has a purpose, it’s not meaningful.
Both these scenarios are common in real data. In scientific research, the purpose of a regression model is one of two things.
One is to understand the relationship between predictors and the response. If so, and if X never = 0, there is no interest in the intercept. It doesn’t tell you anything about the relationship between X and Y.
So whether the value of the intercept is meaningful or not, many times you’re just not interested in it. It’s not answering an actual research question.
The other purpose is prediction. You do need the intercept to calculate predicted values. In market research or data science, there is usually more interest in prediction, so the intercept is more important here.
When A Meaningful Intercept is Important
When X never equals 0, but you want a meaningful intercept, it’s not hard to adjust things to get a meaningful intercept. Simply consider centering X.
Centering sounds fancy, but it’s not. It means to re-scale X so that the mean or some other meaningful value = 0. And all you do to get that is create a new version of X where you just subtract a constant from X. Let’s say X is Age and the mean of Age in your sample 20.
It will look something like: NewX = X — 20.
That’s it.
Just use NewX in your model instead of X. Now the intercept has a meaning. It’s the mean value of Y at the mean value of X.
Interpreting the Intercept in Regression Models with Multiple Xs
It all gets a little trickier when you have more than one X.
The definition still holds: the intercept is the expected value of Y when all X=0.
The emphasis here is on ALL.
And this is where it gets complicated. If all Xs are numerical, it’s an uncommon (though not unheard of) situation for every X to have values of 0. This is often why you’ll hear that intercepts aren’t important or worth interpreting.
But you always have the option to center all numerical Xs to get a meaningful intercept.
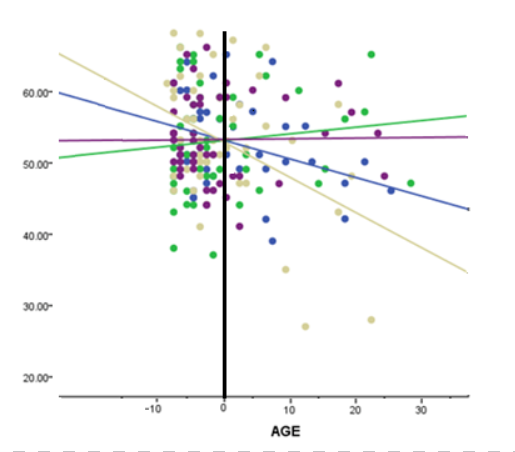
And when some Xs are categorical, the situation is different. Most of the time, categorical variables are dummy coded. Dummy coded variables have values of 0 for the reference group and 1 for the comparison group. Since the intercept is the expected value of Y when X=0, it is the mean value only for the reference group (when all other X=0). So having dummy-coded categorical variables in your model can give the intercept more meaning.
This is especially important to consider when the dummy coded predictor is included in an interaction term. Say for example that X1 is a continuous variable centered at its mean. X2 is a dummy coded predictor, and the model contains an interaction term for X1*X2.
The B value for the intercept is the mean value of X1 only for the reference group. The mean value of X1 for the comparison group is the intercept plus the coefficient for X2.
It’s hard to give an example because it really depends on how X1 and X2 are coded. So I put together six situations in this follow up article: How to Interpret the Intercept in 6 Linear Regression Examples.
Originally published at https://www.theanalysisfactor.com/interpreting-the-intercept-in-a-regression-model. Updated April 10, 2024.
Follow us for weekly articles on data analysis and statistics.
Check out our upcoming FREE webinar on Interpreting Regression Coefficients at https://thecraftofstatisticalanalysis.com/home/.